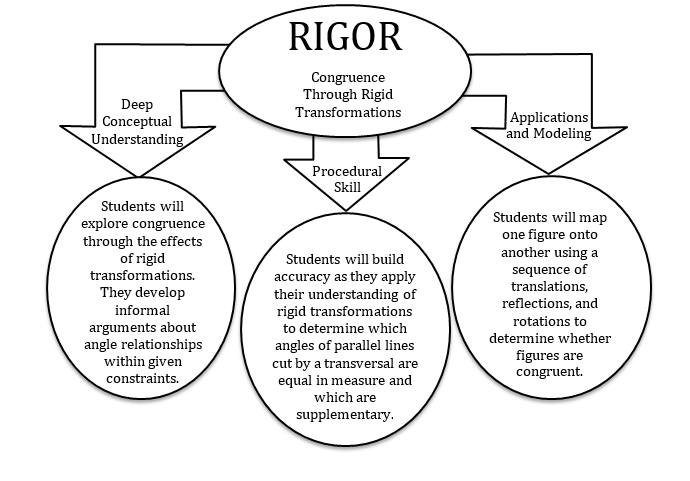
Congruence Through Rigid Transformations
Students will be able to...
- Verify experimentally the properties of rotations, reflections, and translations. Lines taken to lines (1a), line segments to line segments of the same length (1b); angles taken to angles of the same measure; parallel lines taken to parallel lines (1c).
- Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.
*Instructional videos in the hyperlinks above are meant to support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.
In school, your child will…
- Verify
experimentally the properties of rotations, reflections, and translations. Lines taken to lines (1a), line segments to
line segments of the same length (1b); angles taken to angles of the same
measure; parallel lines taken to parallel lines (1c).
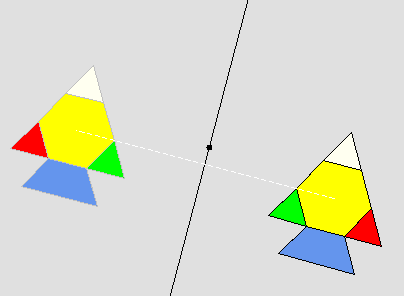
- Visit the online resource, NLVM: Playing with Reflections
- Students click, drag, and rotate the shape on the right as they investigate the properties of rigid transformations.
- Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- Describe
the effect of dilations, translations, rotations, and reflections on
two-dimensional figures using coordinates.
- Describe the sequence of transformations that moves the red triangle to triangle D.
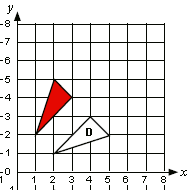
- Describe the sequence of transformations that moves the red triangle to triangle D.
- Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.
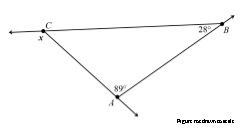
- Find the measure of angle x. Present an informal argument showing that your answer is correct.
At home, your child can…
- Explore the mathematics behind game design as they visit How Did They Make Ms. Pac-Man? After exploring the situation presented, viewers should realize that Ms. Pac-Man is making a series of translations, reflections, and rotations. Discuss how placing the maze onto a coordinate grid can help increase the level of mathematical precision to help you list the path of Ms. Pac-Man.
- Play the Nrich online strategy game, L-ateralThinking. In order to develop a winning strategy to beat the computer every time, players must apply different transformations.
- Visit the CK12 PLIX (Play Learn Interact Xplore):
- Geometric Translations: Transformations of a House
- Reflections: Squiggle Reflections
- Translations, Rotations, and Reflections: Rotate the Triangle
- To access the PLIX, you will need to create a free user account.
Additional Resources
- Khan Academy: Perform Translations Use the interactive transformation tool to perform translations on a coordinate grid. (video tutorial)
- IXL: Shape Mods- Use translations, reflections, and rotations to solve each puzzle. (online game)
- Exploring Rotations through Block Designs (online exploration)
- Grade 8 Standards Unit 7 Topic 1 Congruence Through Rigid Transformations (flexbook)
*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
Similarity Through Non-Rigid Transformations
Students will be able to...
- Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
- Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
*Instructional videos in the hyperlinks above are meant to support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.
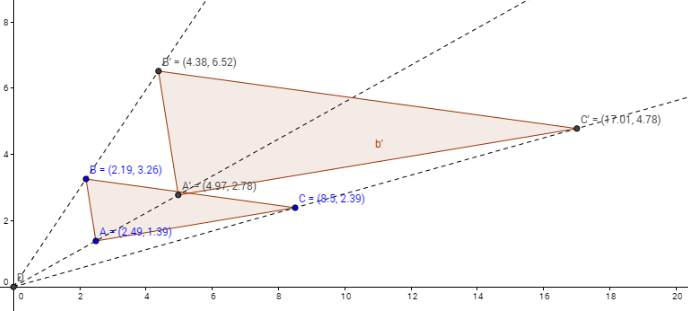
In school, your child will…
- Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- Scale factor: 2
- Center of dilation: The origin
- http://tube.geogebra.org/m/1025645
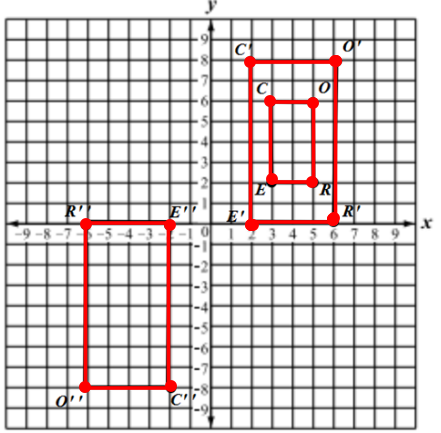
- Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them
- How many transformations have been performed on the figure?
- How do you know which figures are congruent? Similar?
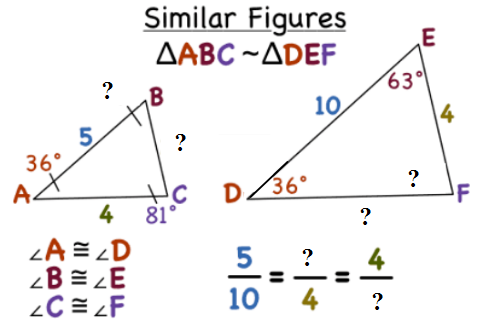
- Use informal arguments to establish facts about the angle-angle criterion for similarity of triangles.
At home, your child can...
Visit the CK12 PLIX (Play Learn Interact Xplore):
- To access the PLIX, you will need to create a free user account.
- Indirect Measurement: Treehouse Height: Use similar triangles to find the height of one object in relationship to another.
- Examine how transformations appear in dance. The online video, Grand Square, showcases two dances that were developed hundreds of years apart.
- Watch as the National Museum of Mathematics uses an image of a visitor to create a "Human Tree" using dilations. This video focuses on how similar figures can create dilations and extends student learning to explore how exponents can be used in an equation to express the proportional relationship in fractals.
Additional Resources
- LearnZillion: Calculate the Scale Factor of a Dilation (video tutorial)
- LearnZillion: Solve word problems by doing dilations (video tutorial)
- Khan Academy: Drawing the Image of a Dilation Example (video tutorial)
- LearnZillion: Prove two figures are similar after a dilation (video tutorial)
- Virtual Nerd: Corresponding Parts of Similar Figures (video tutorial)
- Mangahigh.com - Transtar (online game)
- Mangahigh.com – Similar Shapes (online practice)
- Grade 8 Standards Unit 7 Topic 2 Similarity ThroughNon-Rigid Transformations (flexbook)
*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
Volumes of Cones, Cylinders, and Spheres
Students will be able to...
- Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.
*Instructional videos in the hyperlinks above are meant to support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.
In school, your child will…
- Know the formulas for the volumes of
cones, cylinders, and spheres and use them to solve real-world and mathematical
problems
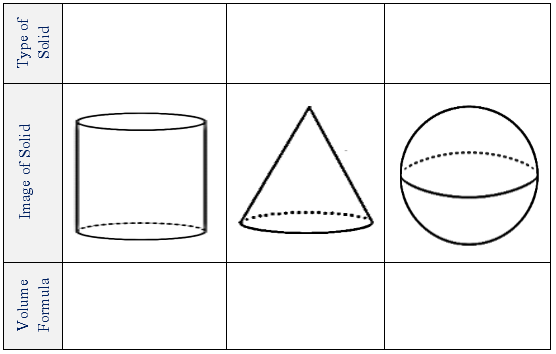
- Name each solid and write the volume formula
- Use the diagram below to
determine which solid has the greater volume.
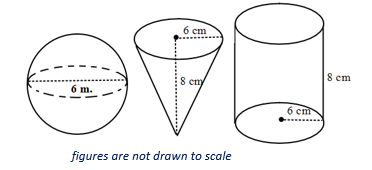
- What is the ratio of the volume of the cone to the volume of the cylinder?
- What is the ratio of the volume of the sphere to the volume of the cylinder?
- Name each solid and write the volume formula
At home, your child can...
- Watch the online video, Understanding Engine Size to see how the volume of cylinders is applied in the real world.
- Take
a trip to the local grocery store and examine which groceries are packaged in
cylinders and which are packaged in rectangular prisms. Then discuss the
following questions together.
- Why do soups and pops and other food containers come in cylindrical containers?
- When food companies ship these items, do they fill the shipping boxes completely?
- When food companies ship these items, what type of package do they use? Is it a cylinder or prism?
- If we ship items in prism boxes for packaging, why do we not make containers that fit this package better? What if we shipped items in prism containers?
Additional Resources
- Mangahigh.com – Volume of a Cylinder (online practice)
- Mangahigh.com – Volume of Spheres (online practice)
- Mathopolis.com – Estimate Volume – Cones (online practice)
- Estimate Volume - Cylinders and Cones (online game)
- Learn
how to develop and apply the formula for:
- Volume of a cylinder by using the concept of stacking circles.
- Volume of a cone by comparing cones to cylinders.
- Volume of a sphere by comparing spheres and cylinders with similar dimensions. (video tutorials)
- Grade 8 Standards Unit 7 Topic 3 Volumes of Cones, Cylinders, andSpheres (flexbook)
*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.