 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
This week your student will be learning to visualize, write, and solve equations. They did this work in previous grades with numbers. In grade 6, we often use a letter called a variable to represent a number whose value is unknown. Diagrams can help us make sense of how quantities are related. Here is an example of such a diagram:

Since 3 pieces are labeled with the same variable
A solution to an equation is a number used in place of the variable that makes the equation true. In the previous example, the solution is 5. Think about substituting 5 for
Solving an equation is a process for finding a solution. Your student will learn that an equation like
Here is a task to try with your student:
Draw a diagram to represent each equation. Then, solve each equation.
Solution:

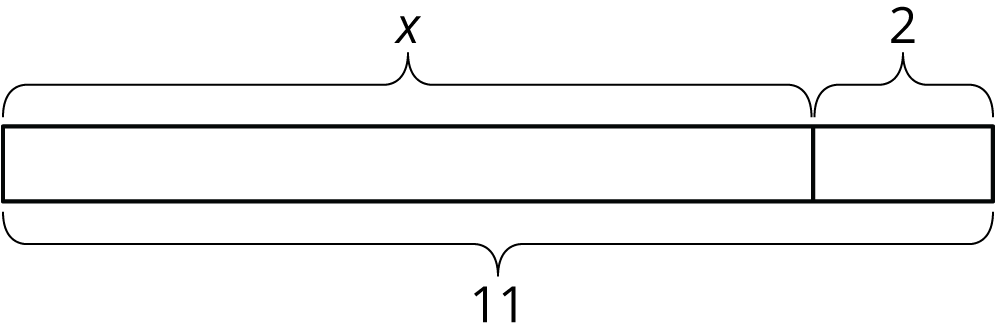
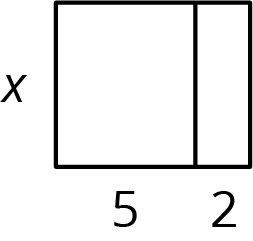
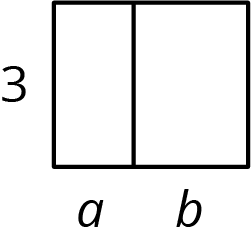
This week your student is writing mathematical expressions, especially expressions using the distributive property.

In this diagram, we can say one side length of the large rectangle is 3 units and the other is
This is an example of the distributive property.
Here is a task to try with your student:
Draw and label a partitioned rectangle to show that each of these equations is always true, no matter the value of the letters.
Solution:
Answers vary. Sample responses:
This week your student will be working with exponents. When we write an expression like
Here is a task to try with your student:
Remember that a solution to an equation is a number that makes the equation true. For example, a solution to
List:
Solution:
This week your student will study relationships between two quantities. For example, since a quarter is worth 25?, we can represent the relationship between the number of quarters,
We can also use a table to represent the situation.
| 1 | 25 |
|---|---|
| 2 | 50 |
| 3 | 75 |
Or we can draw a graph to represent the relationship between the two quantities:

Here is a task to try with your student:
A shopper is buying granola bars. The cost of each granola bar is $0.75.
Solutions
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.