Skip to main content

Mathematics Support

Math 6 | Unit 1 2 3 4 5 6 7 8 9

Unit 5

Arithmetic in Base Ten


Warming Up to Decimals

Multiplying Decimals

Dividing Decimals

 

Warming Up to Decimals

This week, your student will add and subtract numbers using what they know about the meaning of the digits. In earlier grades, your student learned that the 2 in 207.5 represents 2 hundreds, the 7 represents 7 ones, and the 5 represents 5 tenths. We add and subtract the digits that correspond to the same units like hundreds or tenths. For example, to find 10.5+84.3, we add the tens, the ones, and the tenths separately, so 10.5+84.3=90+4+0.8=94.8.

Any time we add digits and the sum is greater than 10, we can “bundle” 10 of them into the next higher unit. For example, 0.9+0.3=1.2.

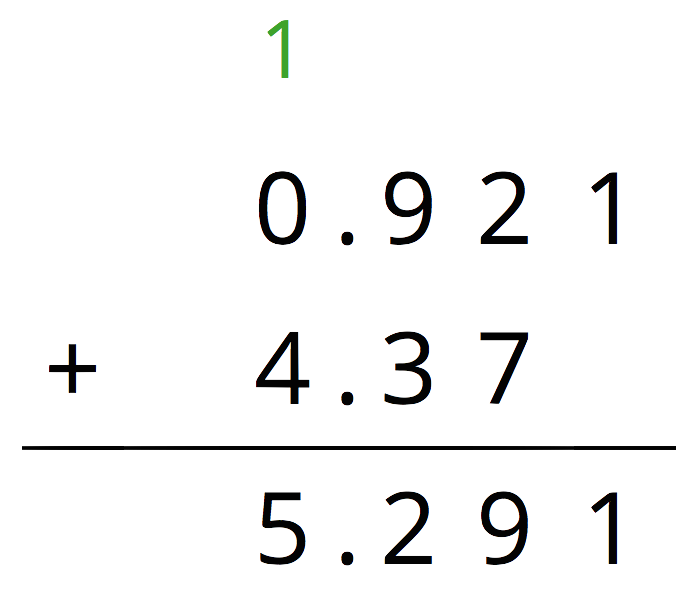
To add whole numbers and decimal numbers, we can arrange 0.921+4.37vertically, aligning the decimal points, and find the sum. This is a convenient way to be sure we are adding digits that correspond to the same units. This also makes it easy to keep track when we bundle 10 units into the next higher unit (some people call this “carrying”).

 

Here is a task to try with your student:

Find the value of 6.54+0.768.

Solution: 7.308. Sample explanation: there are 8 thousandths from 0.768. Next, the 4 hundredths from 6.54 and 6 hundredths from 0.768 combined make 1 tenth. Together with the 5 tenths from 6.54 and the 7 tenths from 0.768 this is 13 tenths total or 1 and 3 tenths. In total, there are 7 ones, 3 tenths, no hundredths, and 8 thousandths.

Multiplying Decimals

This week, your student will multiply decimals. There are a few ways we can multiply two decimals such as (2.4)⋅(1.3). We can represent the product as the area of a rectangle. If 2.4 and 1.3 are the side lengths of a rectangle, the product (2.4)⋅(1.3) is its area. To find the area, it helps to decompose the rectangle into smaller rectangles by breaking the side lengths apart by place value. The sum of the areas of all of the smaller rectangles, 3.12, is the total area.

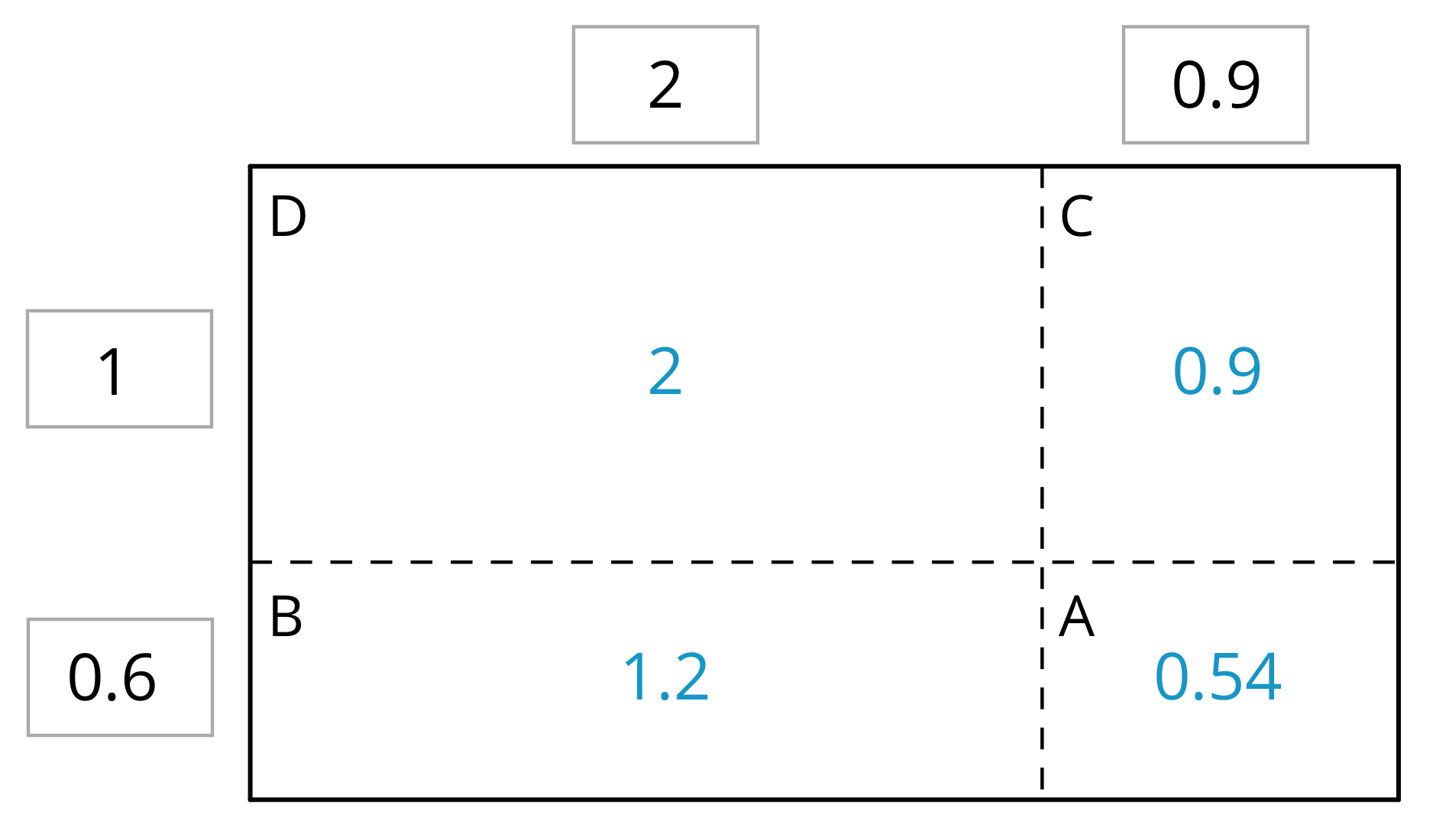
Here is a task to try with your student:

Find (2.9)⋅(1.6) using an area model and partial products.

Solution: 4.64. The area of the rectangle (or the sum of the partial products) is: 2+0.9+1.2+0.54=4.64

Dividing Decimals

This week, your student will divide whole numbers and decimals. We can think about division as breaking apart a number into equal-size groups.

For example, consider 65÷4. We can image that we are sharing 65 grams of gold equally among 4 people. Here is one way to think about this:

  • First give everyone 10 grams. Then 40 grams have been shared out, and 25 grams are left over. We can see this in the first example.
  • If we give everyone 6 more grams, then 24 grams have been shared out, and 1 gram is left.
  • If we give everyone 0.2 more grams, then 0.8 grams are shared out and 0.2 grams are left.
  • If everyone gets 0.05 more grams next, then all of the gold has been shared equally.

Everyone gets 10+6+0.2+0.05=16.25 grams of gold.

The calculation on the right shows different intermediate steps, but the quotient is the same. This approach is called the partial quotients method for dividing.

Here is a task to try with your student:

Here is how Jada found 784÷7 using the partial quotient method.??

  1. In the calculation, what does the subtraction of 700 represent?
  2. Above the dividend 784, we see the numbers 100, 10, and 2. What do they represent?
  3. How can we check if 112 if the correct quotient for 784÷7?

Solution

  1. Subtraction of 7 groups of 100 from 784.
  2. 100, 10, and 2 are the amounts distributed into each group over 3 rounds of dividing.
  3. We can multiply 7⋅112 and see if it produces 784.
 

IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.

Disclaimer: This site provides external links and videos as a convenience and for informational purposes only. The appearance of external hyperlinks on the MCPS Family Mathematics Support Center website does not constitute an endorsement by the Montgomery County Public School System of any of the products or opinions contained therein.