 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
This week, your student will be thinking about the meanings of division to prepare to learn about division of fraction. Suppose we have 10 liters of water to divide into equal-size groups. We can think of the division
Here are two diagrams to show the two interpretations of

In both cases, the answer to the question is 5, but it could either mean “there are 5 bottles with 2 liters in each” or “there are 5 liters in each of the 2 bottles.”
Here is a task to try with your student:
Solution:
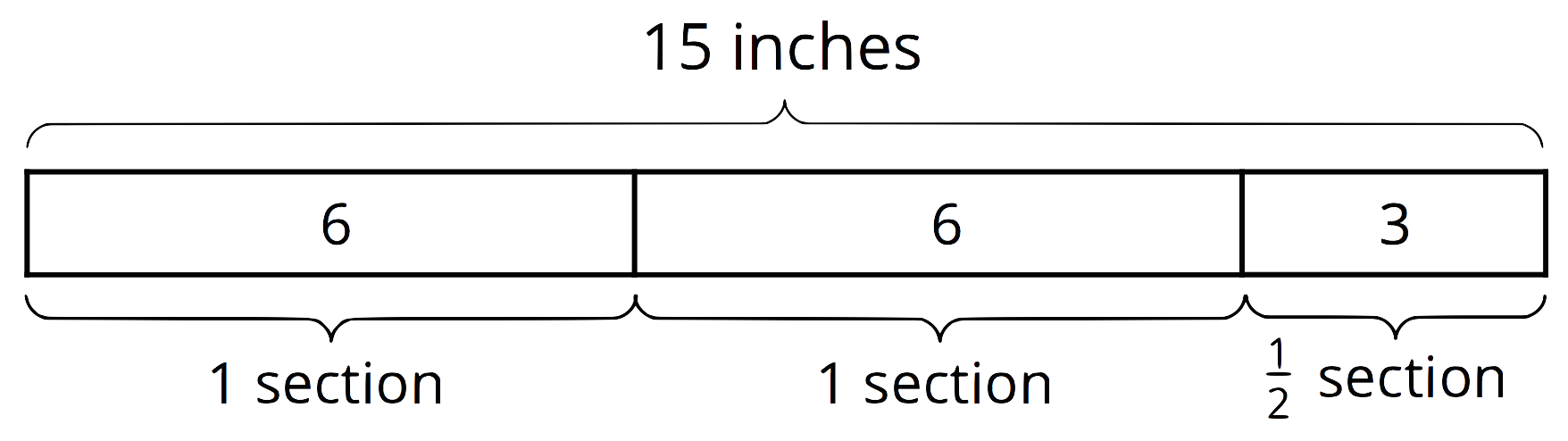
Earlier, students learned that a division such as
This week, they use these ideas to divide fractions. For example,
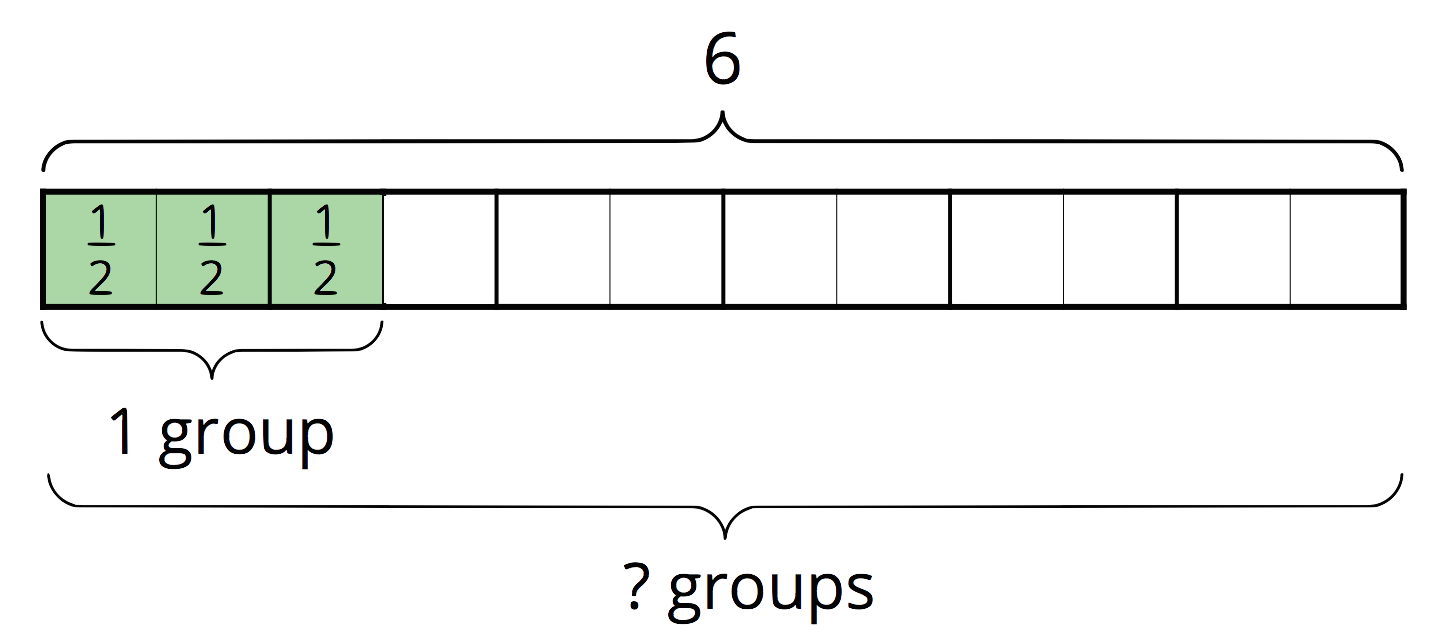
From the diagram we can count that there are 4 groups of
We can also think of
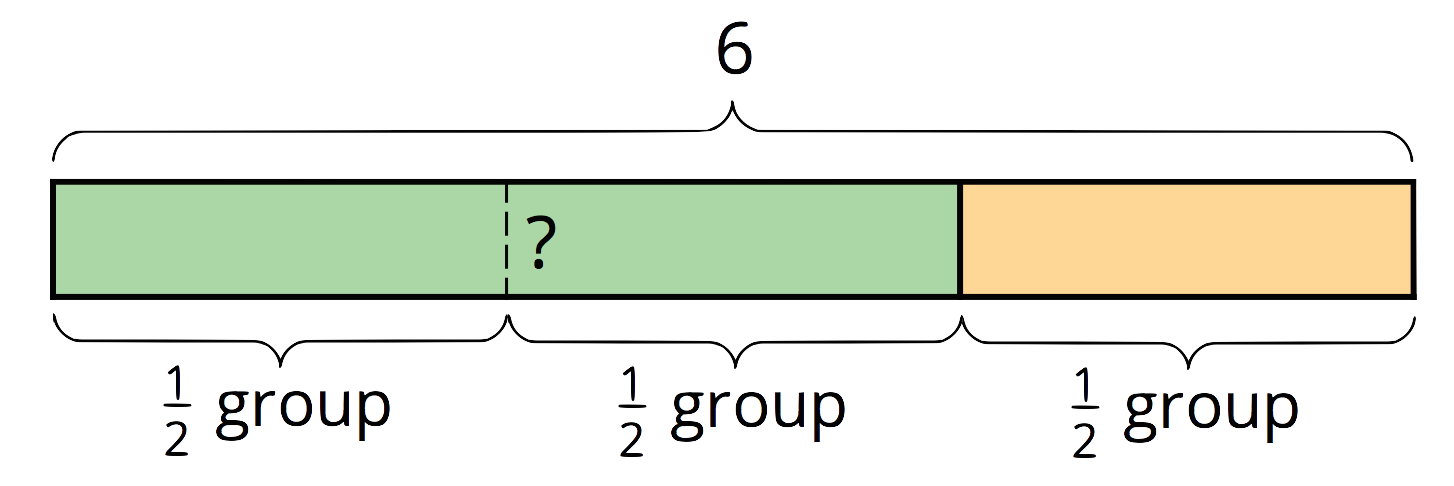
From the diagram we can see that if there are three
In both cases
Here is a task to try with your student:
Solution:
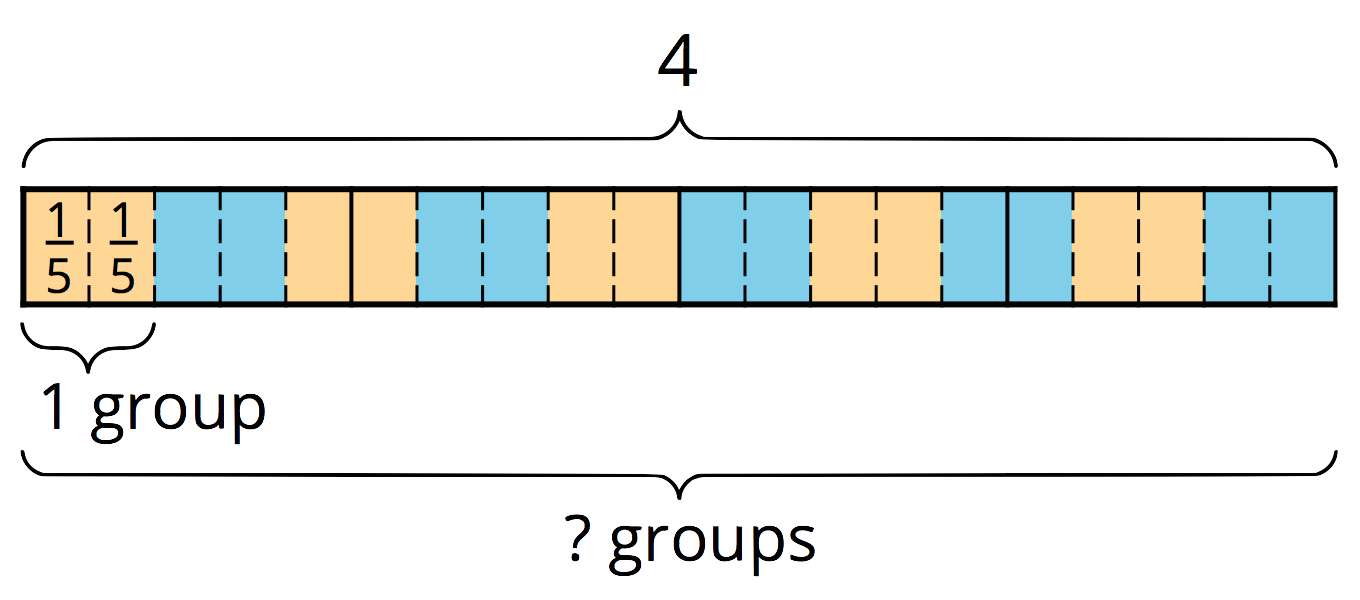
Many people have learned that to divide a fraction, we “invert and multiply.” This week, your student will learn why this works by studying a series of division statements and diagrams such as these:
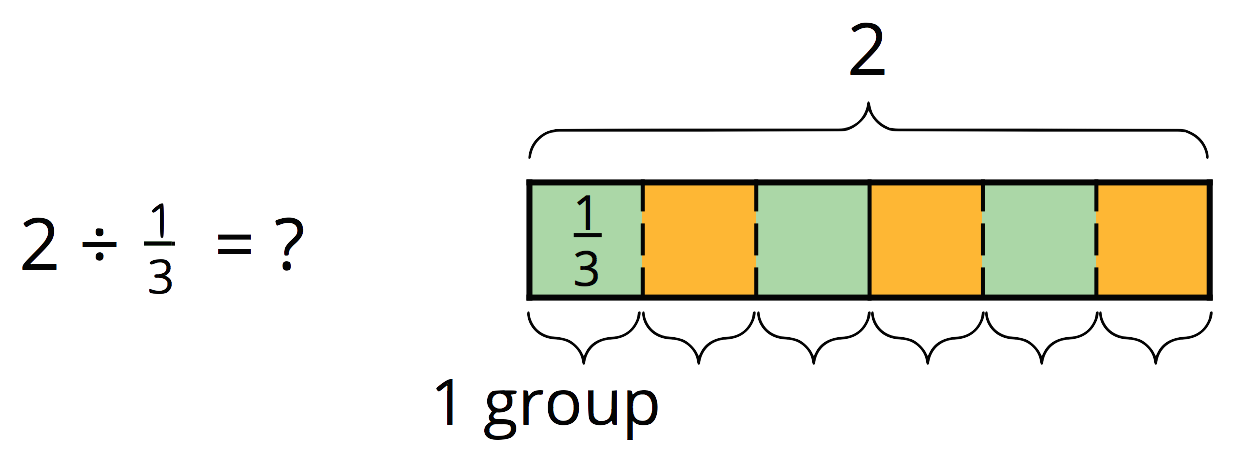
Because there are 3 thirds in 1, there are
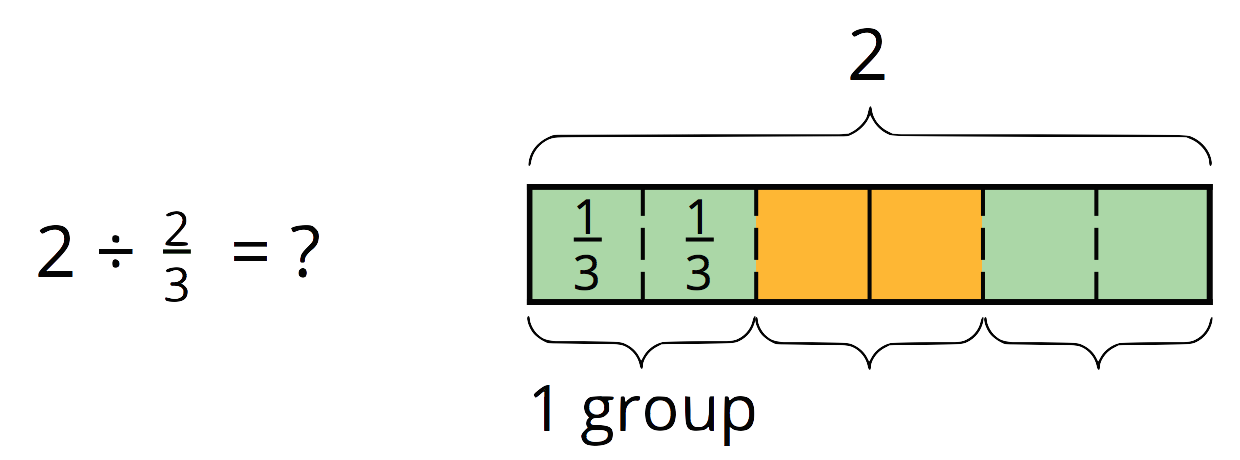
We already know that there are
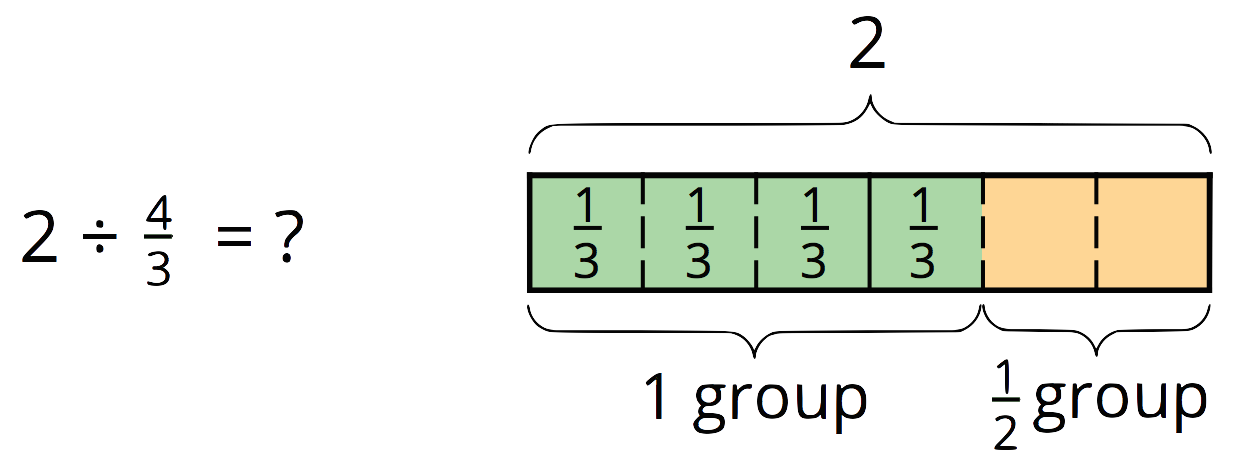
Again, we know that there are
Notice that each division problem above can be answered by multiplying 2 by the denominator of the divisor and then dividing it by the numerator. So
Here is a task to try with your student:
Solution:
Over the next few days, your student will be solving problems that require multiplying and dividing fractions. Some of these problems will be about comparison. For example:
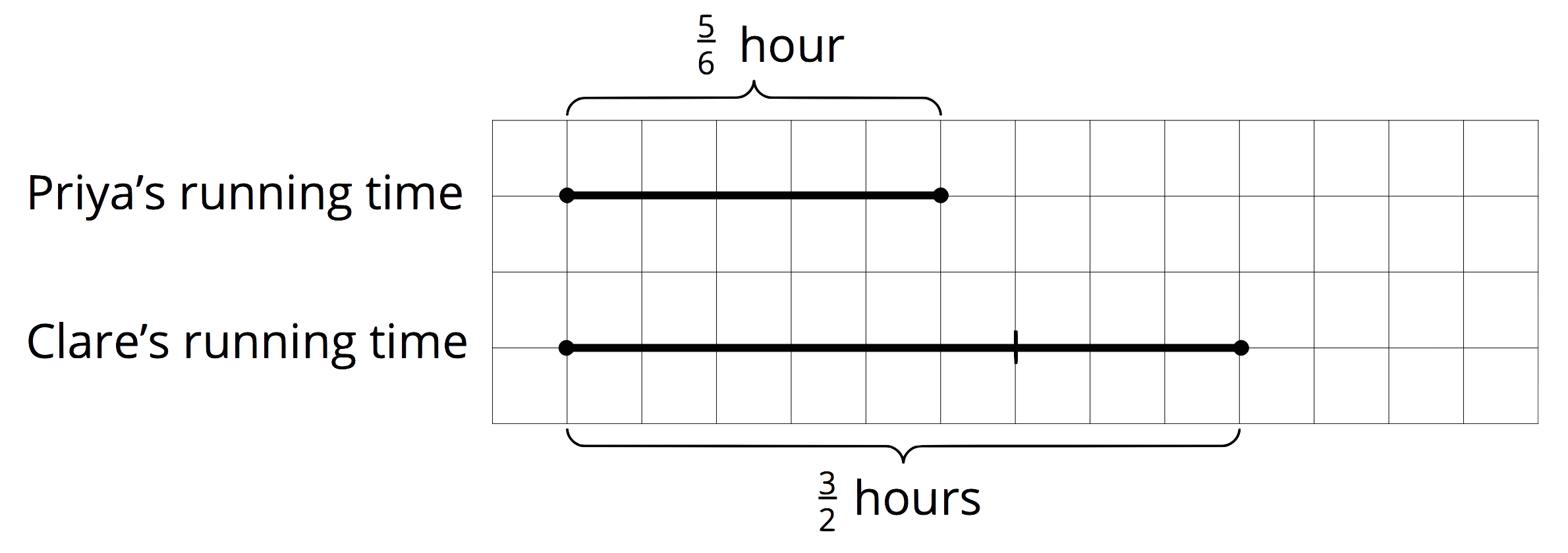
If Priya ran for
We can draw a diagram and write a multiplication equation to make sense of the situation.
Other problems your students will solve are related to geometry—lengths, areas, and volumes. For examples:
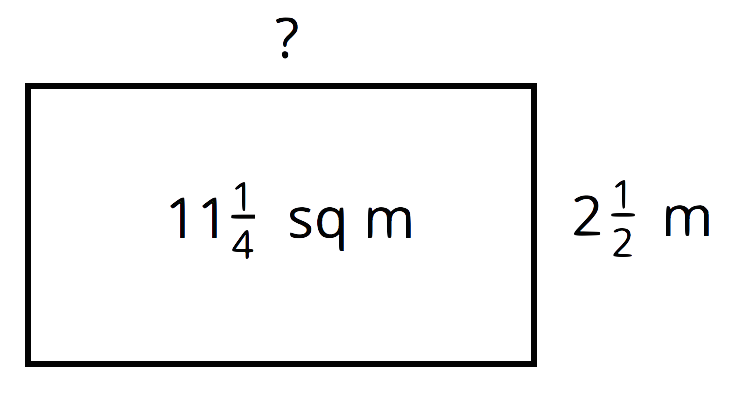
We know that the area of a rectangle can be found by multiplying its length and width (
What is the volume of a box (a rectangular prism) that is
We can find the volume by multiplying the edge lengths.
Here is a task to try with your student:
Solution:
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.