 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
This week your student will learn why circles are different from other shapes, such as triangles and squares. Circles are perfectly round because they are made up of all the points that are the same distance away from a center.
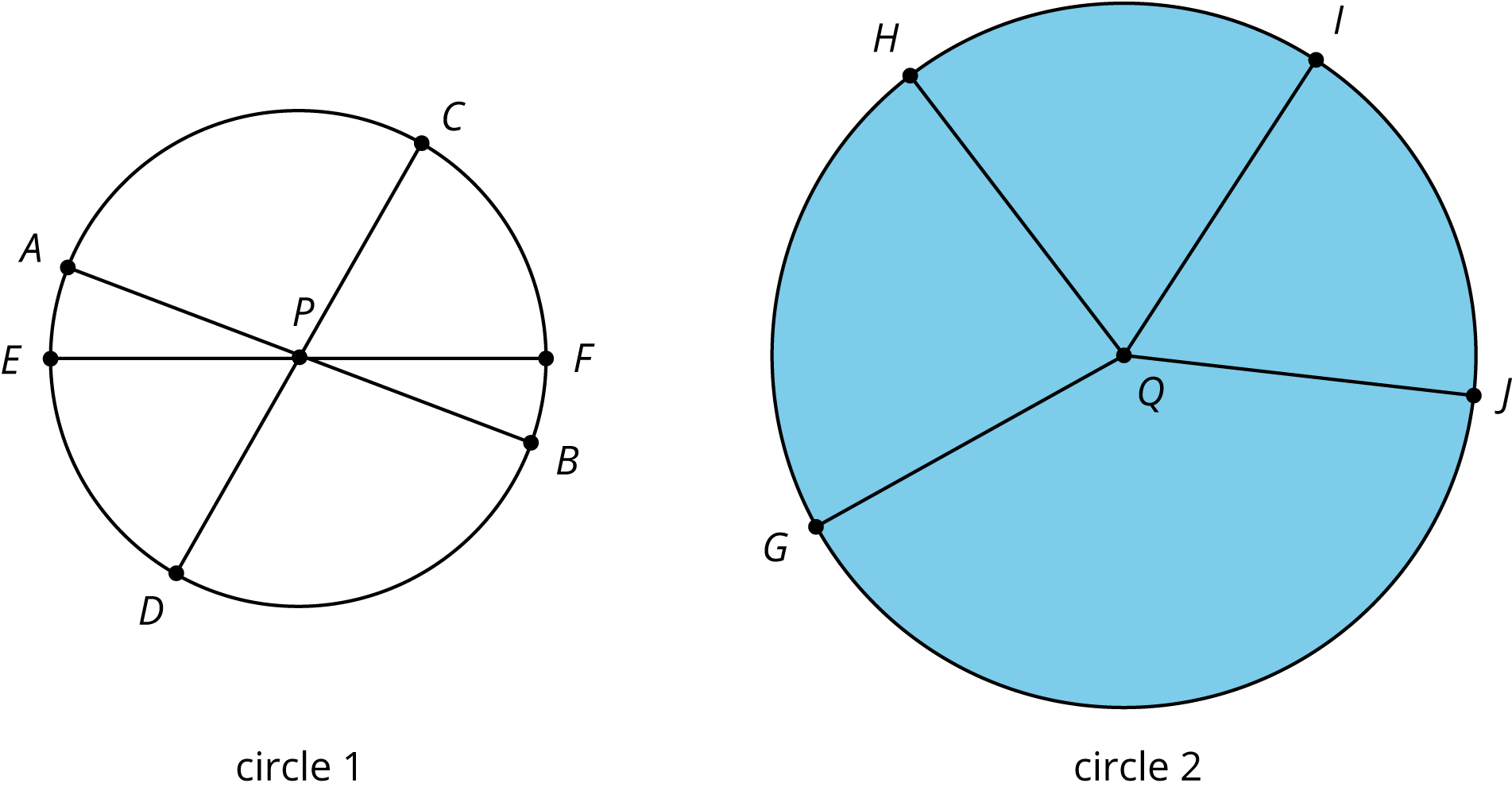
We can use the proportional relationships between radius, diameter, and circumference to solve problems.
Here is a task to try with your student:
A cereal bowl has a diameter of 16 centimeters.
Solution:
This week your student will solve problems about the area inside circles. We can cut a circle into wedges and rearrange the pieces without changing the area of the shape. The smaller we cut the wedges, the more the rearranged shape looks like a parallelogram.
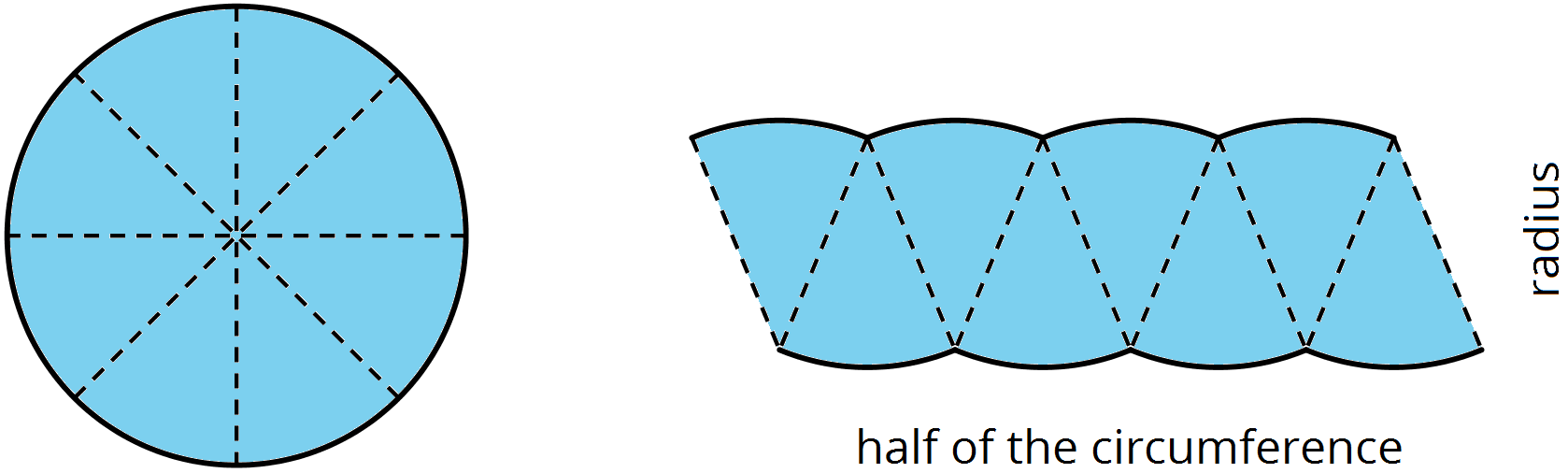
The area of a circle can be found by multiplying half of the circumference times the radius. Using
Or
This means that if we know the radius, we can find the area. For example, if a circle has radius 10 cm, then the area is about 314 cm2, because
Here is a task to try with your student:
A rectangular wooden board, 20 inches wide and 40 inches long, has a circular hole cut out of it.
Solution:
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.