 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
 MONTGOMERY COUNTY PUBLIC SCHOOLS
MONTGOMERY COUNTY PUBLIC SCHOOLS
The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.
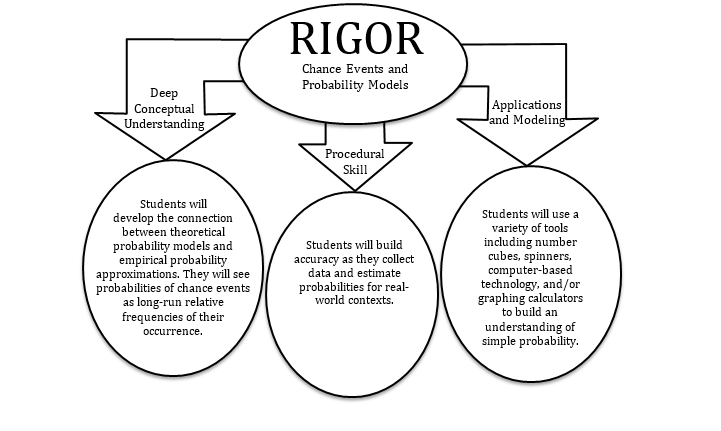
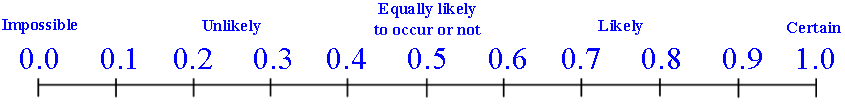

*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
*Instructional videos in the hyperlinks above are meant to support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
The Common Core State Standards require a balance of three fundamental components that result in rigorous mathematics acquisition: deep conceptual understanding, procedural skill, and mathematical applications and modeling.
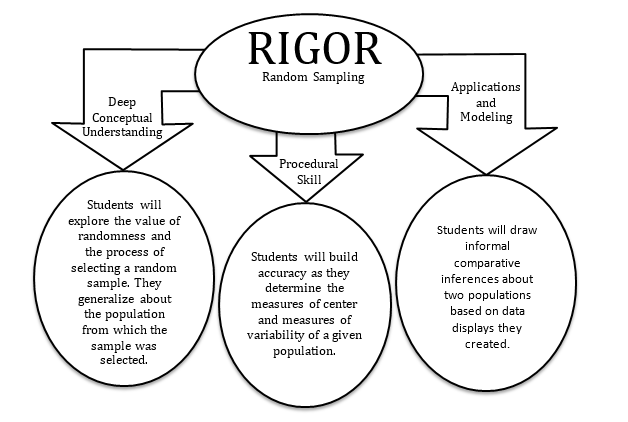
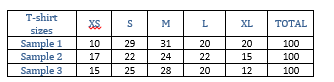
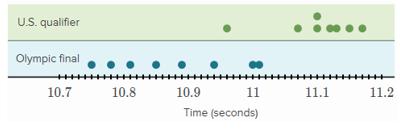
LearnZillion: Drawing Inferences about a Population (video tutorial)
*Additional Practice links support C2.0 content, but may use vocabulary or strategies not emphasized by MCPS.
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.